[Awaiting Admin Approval] [nutki] 32bit precision entry (1012B, 58 days, 20 hours before the deadline)
Posted by [sgstair], Started at 2008-03-29 00:00:00 (Competition Ended 6350 days, 23 hours ago.)
Hello everyone, and welcome to the first contest, in the new Akkit.org optimization contest website!This has been a long road, but finally the site has been put together and all of the necessary prerequisites are in place for the first contest.
Some of you may realize that the idea for this site was formed in November 2007, and it's taken me a lot of time to get it all set up, but now I'm ready to unveil the first topic, which has been waiting for this website for almost 6 months now :)
Please note that this site is a work in progress, and is brand-new, completely written from scratch.
I consider myself to be pretty good about php development so I doubt there are any security vulnerabilities, though if you do find one, please let me know ;)
If you think the problem statement is not sufficient, or have other problems related to the contest, please let me know as well.
Hint: A good way to let me know is to post comments!
Hint 2: If you can't register for whatever reason, try the contact info on the Main Page
Problem Statement
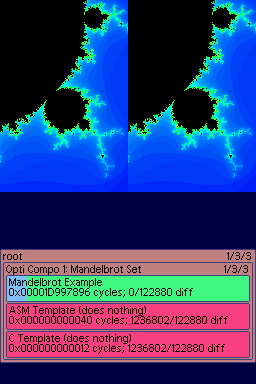
The test program (v4) in action.
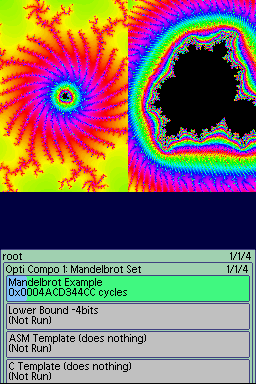
The last 2 tests from v5.
First of all, this is a speed optimisation contest; so, the winner will be the entry which completes the tasks set before it the fastest. There are lots of ways to improve the speed of such a process, and it's a classical mathematical and computer programming problem, so I thought this was appropriate to start the competition with.
Here are the specific requirements of the code to be optimized:
* It needs to plot a rectangular section of the Mandelbrot set into an array (That array may be rotated or scaled, it's not axis-aligned)
* The rectangular section will be defined by top left point ( a complex value ), complex step values in the X and Y directions, and the width and height (in array elements) of the output
* The top left point and step values will be complex numbers represented by 2 64bit values (one for the real, one for imaginary dimension), each value being defined as a 4:60 precision fixed point number (-8 to +7.999...)
* The output array will be an array of 16bit values corresponding to the number of iterations before the value at that point diverges (up to some cap given in the function parameters) (this is defined more specificly in the section below)
* You will be given a 512kiB block of contiguous memory, which is aligned to a cache line boundary. You don't have to use it, but if you need to use a lot of memory, it's where you should be putting things.
* Regarding precision: You must keep 64bits of precision through all operations, the C code will do this, so if you don't, your submission will probably be disqualified. Without some guarantees on precision, the code isn't going to be very useful. Also, since it's a speed optimisation contest, you are welcome to make your code more precise, but you're probably better off not doing so. Good luck! A small amount of difference is understandable, too, given differences in math that can be used, so your output won't have to be exactly like the example code, just not completely different.
* Here's the function prototype for the function that does all this: void MandelFunc(u32 * rectangle, int max_iteration, int width, int height, u16 * output_array, void * workram);
* Rectangle is a list of 64bit numbers, 64bit numbers are stored as the low 32bits followed by the high 32 bits - the numbers are topleft_real, topleft_imaginary, stepx_real, stepx_imaginary, stepy_real, stepy_imaginary (total of 6 64bit values, or 48 bytes)
To make this process a lot simpler, I've written a small program for DS that can run code snippets in a rather controlled environment. It's in a zip file package below. This package contains the test engine, which is a bit hacky and slow ;), it also contains 2 other important elements: the example C++ code that does everything an entry needs to (you could submit it if you want, but then we might laugh at you.) - also included are some templates, bare bones C++ and asm files that show you how to start your own routine. The test app can be easily built with the latest versions of devkitARM and libnds, and will allow you to test the speed of one or more implementations you have created. The test app uses seeded random data to compare the output of your functions to the reference function, so you also get verification of whether or not your code is working correctly.
Download the Source package here (version 5) - This includes a test application which has a reference implementation of the function to be optimised as well as some templates to choose from.
Note about the source package: First version was really rushed and missed a trivial optimisation - so version 2 of the package has been released with example code that's roughly 6 times faster - It will no longer be quite so painful to test things, previously this code was a limiting factor for testing, taking 30+ seconds to verify the tests, now it should only be around 5 seconds.
Note 2: Version 3 fixes a glaring bug in the fixed point multiply. On a related note, precision isn't tested very well in the current test package, there will be another test project release in a few weeks that will better verify precision. Version 4 fixes a sign error in the multiply which I really should have seen (thanks pepsiman and nutki)
Verstion 5: v5 fixes a bug in the timing (it was displaying only the last test's time), updates the default test to be a zoom in on a specific location (6 tests, each more zoomed in than the last), and provides a lower bound for correctness. So now the correctness of an implementation should be much easier to validate - also in this build is a feature where pressing start instead of A will run the tests without comparing them to the reference implementation, for quicker testing. Tests in this version are much slower though, because the rendering is deeper and more complex.
Now, about Rules:
Every compo needs 'em!
CAN means you may; SHOULD means you are probably missing out if you don't, MUST and MUST NOT indicate mandates from the heavens; ask me before doing the opposite and be prepared to be told not to.
* You MUST NOT use any global variables (besides constant data)
* You MUST NOT put any code or constant data in ITCM or DTCM
* You CAN have constant data, but not too much, 64k is more than enough space
* You CAN use the hardware divide / sqrt capabilities of the DS
* You MUST NOT use timers, graphics hardware, or other DS hardware outside of the hardware math functionality. I can't think of any useful exceptions but may be willing to grant some if I'm wrong.
* You CAN use malloc/free/new/delete, and other standard library functions in either the C or C++ standard libraries. It's your cputime, who am I to stop you ;)
* You CAN use stack-allocated memory, just be aware that the full 16k of DTCM (where the stack resides) may not be available to you.
* Your code can't be too terribly big. I'm thinking 64k is the threshhold of "starting to get too big" and 128k is the threshhold for "yeah, that's just too big." - if you do manage to use that many instructions though, you won't lose that much speed by halving the size of your unrolled loop anyway :P (And I mean compiled size, not source size)
About the Mandelbrot set
I'm sure some of you have run into the Mandelbrot set before, either plotting it with some trivial code or just tinkering with some fractal generator, but it's unlikely you remember exactly how it works off the top of your head. So, this section is all about how it works.The Mandelbrot set is a fairly simple relationship based on complex numbers (see link for more info). In short, complex numbers are 2-dimensional numbers, with one dimension in the "real" plane (normal numbers), and one dimension in the "imaginary" plane (numbers multiplied by "i", or sqrt(-1) ).
So, adding and subtracting complex numbers works a lot like normal 2d vectors; (a+b*i) + (c+d*i) = ( (a+c) + (b+d)*i )
Multiplication and division are more complex though. Multiplication winds up looking like a polynomial expansion: (a+b*i) * (c+d*i) = a*c + a*d*i + b*c*i + b*d*i*i, and since i*i is -1, you're left with = (a*c - b*d) + (a*d + b*c)*i;
And division is even more complex, requiring first a step to reduce the denominator to a real number: (a+b*i) / (c+d*i) = (a+b*i)*(c-d*i) / (c+d*i)*(c-d*i) = ((a*c+b*d)+(b*c-a*d)*i) / (c*c+d*d) - Which is just a multiplication problem and division by a constant, so I won't complete the expansion here.
Fortunately, the Mandelbrot set only uses Multiplication and Addition, which are both generally pretty easy.
Specificly the Mandelbrot set consists of all of the points in the complex plane where a specific recursive relation never diverges to infinity. The relation that defines the Mandelbrot set is P(n+1) = P(n)*P(n) + c, where P(0) is 0, and c is the value of the point you're testing in the complex plane.
The Mandelbrot set exists completely inside a circle with radius 2, the furthest point in the set is (-2 + 0*i), so if P(n) is ever outside of that circle, we know that point will converge to infinity and not be in the Mandelbrot set.
We're not purely interested in whether the points are in the set though, we want to know how many iterations it took if they were pushed out of that circle, that's how we get the fancy colors! So, for this problem store the first "n" that was outside of the radius-2 circle into the 16bit array value for that location. You will be given a "maximum" value, and if your n passes the maximum value, you should set the maximum value for that array element and move on.
Wrapping it up
Ok, this description went on a lot further than I expected!I do realize that this is a pretty tough problem! If you'd like to be involved in an optimization contest but this is too hard, tell me! I'm currently considering opening up a second "branch" of competitions, for easier optimization contests, and whether I do will depend on if anyone bugs me about it!
This competition is going to be running for 2 months - which should be long enough to implement and optimize something like this; I'm mostly using 2 months because I figure I'll have more time around then, the next month looks pretty hectic for me.
Also, I have planned to create an update for the test application, to allow timer-sampled profiling (with profiler in ITCM so it doesn't screw up the cache profiling much), which should prove a powerful tool for finding issues and optimizing code! look for that around a month from now.
Notable Questions
I've received a significant question that I think the answer should be easy to access, so I've added this section to keep track of important questions and their answers:Question: Is it ok to use other people's publicly available code for this competition?
Answer: Technically yes; as long as it has a license that's compatible. See the Rules page... Just copying the code goes against the spirit of this competition site, the goal is to learn something and produce new code; but I won't disallow it.
Question: Can entrants work in teams?
Answer: Yes. Only one account may be tied to an entry though, so you'll have to credit teammates in the title or the source code that's submitted. (Inappropriate team names may be moderated, you know who you are :P)
Question: What do I have to submit to enter?
Answer: Only the source files you created/modified, in one of the supported archive formats (zip, rar, tar)
Question: Will there be prizes?
Answer: Not in this competition. I'm considering it for future competitions though.
Question: Will you (sgstair) be entering?
Answer: I will likely work on my own solution and submit it, but my entry will be unranked.